EMNLP/CoNLL
Baby Bayesians? Evidence for Statistical Hypothesis Selection in Infant Language Learning
LouAnn Gerken
- Experimental peradigm: familiarization -- present the infants with new linguistic stimuli for ~2min. flashing light at 3 locations -- teach the baby to look where the light is. only present linguistic stimulus when they're attending to a given light. so measure how long the child attends to each stimulus. try it with the same sound from the familiarization; or with something different.
Prior work:
- infants attend to word lists from their own language longer than to lists from related languages that violate the phonetic rules of their language.
- infants listen longer to novel (made-up) words with higher probability phonotactics
- string together a fixed lexicon of 4-syllable made-up words, and see if babies can distinguish the words from random strings over the same sounds.. they can.
- pick 2 closely related phonemenes, and continuously vary between them.. In familiarization, try presenting the continuous space with a unimodal or bimodal distribution.. Babies in bimodal distribution learn to distinguish them.
- given strings AXB, where X varies, babies will learn to generalize iff {X} is large enough (~24 elts)
Q: how do babies generalize? Give them stimuli that could be generalized in different ways, and see how they generalize it.
more prior work:
- define 4 syllables {A} and 4 {B}; and generate words AAB for one set of babies and ABA for another set. Then present both to the babies, using new sets of syllables, and see what they generalize to. Babies attend more to the words that are consistent with the pattern that they learned.
terminology: consistent = babies hearing what they were familiarized with; inconsistent = novel to the baby.
- variation: if
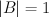 (there's just one B elt), then babies can, and do, make the less abstract generalization. I.e., rather than learning the pattern AAB, they learn the pattern AA/di/ (where B={/di/})
(there's just one B elt), then babies can, and do, make the less abstract generalization. I.e., rather than learning the pattern AAB, they learn the pattern AA/di/ (where B={/di/})
two theories:
- model selection -- babies are choosing between models of their input
- single generalization -- babies commit to one generalization
infants choose among generalizations, and make the one that's conservative given the data. they are capable of moving from one generalization to another based on a fairly small number of inputs. (c.f., bayesian hypothesis selection)
Hashing, Sketching, and other approxiamte alogorithms for high-dimensional data
Piotr Indyk, MIT
Use randomized algorithms to handle very large data sets. Basic technique shared by algorithms: randomized projection. Focus on two problems for high dimensional data:
- Storage -- how do we represent the high-dimentional data "accurately" in a "small" amount of space?
- Search -- how do we find similar entries in the high-dimensional data?
Randomized dimensionality reduction (aka randomized projection)
- choose the projection plane "at random"
- distances are "approximately" preserved w/ "high" probability (Johnsons-Lindenstrauss lemma 1984 = flattening lemma).
There exists a distribution over random linear mappings 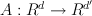 such that when we apply the linear mapping, the distance of vectors is preserved within a small
such that when we apply the linear mapping, the distance of vectors is preserved within a small  .
.
One such distribution is the normal distribution.
References
nearest neighbor in high dimensions:
- CRC Handbook '03
- CACM Survey
Streaming:
- Survey: S. Muthukrishnan
- Summer school +materials: Google "Madalgo"
slides will be on website