| Tags: | |
|---|---|
| Webpage: | http://ssl-acl08.wikidot.com |
| Presenter: | John Blitzer |
| Authors: | John Blitzer and Xiaojin (Jerry) Zhu |
| Date: | June 15th, 2008 |
ACL 2008: Semi-Supervised Learning Tutorial
Basic task: use unlabeled data to improve performance on a supervised learning task.
Arguments against SSL
- For important problems, we'll find the time/money/manpower to label more data. (expensive. how much is enough? For Chinese treebank, it took 4 years to label 4k sentences.)
- Cover 1996: for a specific class of generative models, labeled samples are exponentially more useful than unlabeled. (but doesn't apply to all models)
Arguments for SSL
- Can't afford to label a lot of data; or
- Have a lot of labeled data; but even more unlabeled data.
- Domain adaptation
Bootstrapping
Notation:
- labeled instance pairs
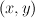
- learners or hypotheses h or f:
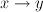
- labeled data =
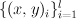
- unlabeled data =
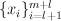
On labeled error, minimize error. On unlabeled data, minimize a proxy for error that's derived from the current model.
- Train model un labeled data
Repeat until convergance:
- label unlabeled data with current model
- retrain w/ unlabeled data
When applied to naive bayes: e.g., if we learn that "Mr. <foo>" is a person, then we can learn instances of <foo>. (This will, of course, depend on our features.)
Folk wisdom
- works better for generative than discriminative features. (overfitting?)
- works better when naive Bayes assumption is stronger.
Explaining the folk wisdom: assume that there are two views of a problem, and each is sufficient to do good classification. E.g., context vs content. As long as this is true, we can do reasonable learning from unlabeled data, by using context to find good contents, and vice versa.
So we're maximizing accuracy on the labeled data, and then adding the constraint that the two views must agree with one another.
Co-boosting (Collins and Singer 1999)
Boosting:
- define one base model
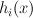 for each feature, which is true where that feature is true.
for each feature, which is true where that feature is true. - on each round, choose a base model, and assign a weight
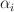 for it.
for it. - final model has the form:
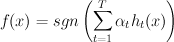
normal boosting: pick 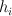 and
and 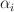 to minimize error (see slide 17)
to minimize error (see slide 17)

(laptop battery died)
Graph-regularization
- if we can pick a good graph, then it helps. But it can be hard to tell a priori whether a graph is good or not.
Structural learning
- use unlabeled data to constrain the structure of the hypothesis space
- use unlabeled data & auxiliary problems to learn a representation
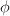 , an approximation of span(W)
, an approximation of span(W)- for each feature, mask that feature, and use the remaining features to predict that feature.
- this gives us n linear predictors, one for each binary problem (feature)
- these weights give us info about the conditional covariance structure -- i.e., which of the features covary with one another.
- so when we map to a lower-dimensional representation, we want the features that covary to be mapped to similar areas in the lower-dimensional representation.
- do dimensionality reduction. We start with W, where multiplying W by x gives us predictions of the features.. Then use SVD to reduce dimensionality.
- use labeled data to learn weights for the new representation
- use unlabeled data & auxiliary problems to learn a representation
given a target problem (eg entity classification), design some auxiliary problems which are different but similar, and can be trained on unlabeled data. Regularize the target problem hypothesis to be close to the auxiliary problem hypothesis space.
example: for named entity classification, predict the presence or absence of words in a specific context location (eg word i-1, word i, word i+1).
example: for sentiment classificaiton, predict the presence/absence of frequent words (eg horrible, suffering, dont_waste).
In a sense, it seems like we're defining classifiers that try to predict our feature vector..
Define the matrix whose columns are weight vectors for the auxiliary problems.
Then given a new hypothesis weight vector v, how far is it from span(W).
We learn the weight vector v, picking out which of the lower-dimensionality features are actually useful -- this is important, because different pieces will be different for different domains.
structural learning gives a significant improvement even with large amounts of labeled data -- c.f. with eg co-training, which is mostly helpful if we don't have much labeled data.
Why does structural learning work?
- Good auxiliary problems gives us a good representation
- structural learning seperates unsupervised & supervised learning, which leads to a more stable solution
- if we make a mistake in choosing the representation (e.g., select a dimension of our lower-dimensional feature vector that's not useful), then we can recover by just ignoring it.
- structural learning can be used when auxiliary problems are obvious, but the graph structure is not
- adding more unlabeled data will always help with structural learning (c.f. bootstrapping, where more data increases recall but drops precision).
- we're basically allowing the model to use two types of features: features on the original model, which are penalized, and features on the lower-dimensional features that we got from the unlabeled data, which are not penalized.
- there's an intuition here that this is similar to choosing a feature vector that's close to the span of the low-dimensional thingy. But it's not quite the same.
- it can be necessary to do some re-weighting of the positive and negative instances for the lower-dimensional features, because otherwise the model will just decide that everything is negative or everything is positive.
What can go wrong with structural learning?
For some problems, it's hard to define good auxiliary problems.
we're combining real-valued & binary features:
[-----------x------------|--phi*x--]
The x part is binary, high-dimensional, and sparse; the phi*x part is real-valued, low-dimensional, and dense. This can cause issues for some learning systems.