Fast Algorithms for Large-State-Space HMMs with Applications to Web Usage Analysis
CHECK YEAR!
This paper shows how basic HMM operations can be made more efficient in the special case where the transition probabilities can be expressed as a simple distance metric between states. In particular, the basic operations are reduced from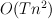 
to 
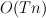, where 
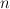is the number of states. This is useful in cases where:
- We want to use states to discretize one or more continuous variables.
- We want to use a large number of states.
The first bullet point (states that discretize continuous variables) is what justifies the use of a distance metric to define transition probabilities: if our states are symbolic, or related to each other in complex ways, then it's unlikely we will be able to find any simple distance metric that tells us how likely we are to transition from one state to another. But if states correspond to some space, then the use of a distance metric makes more sense. E.g., if we use states to represent locations where a robot might be in a room, then it's sensible to define a distance metric between them.
The second bullet point is what makes this worth-while -- if the number of states (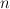) is large, then reducing the time of these operations from 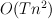to 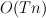will result in significant time savings.
How it works
The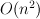 
step in Viterbi-like algorithms comes from searching for the maximum-probability transition between a pair of states. I.e., for each 
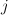we must find: 
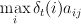. Transforming this to log space, we can equivalently find the min of a sum: 
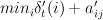. To do this in the general case, we must check every value of 
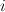. But if 
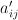is defined as a function, then we may be able to find the minimum in constant time, depending on the properties of that function.
In particular, Felzenszwalb present several functions such that this minimization can be done in constant time, or done approximately in constant time. This is what reduces the running time of the basic HMM operations.
Example
Consider an HMM that describes interest in a downloadable item over time, where each state corresponds to a discretized level of interest; and observations are binary values indicating whether a user who looked at the item's description decided to download it. We choose a distance metric that says that normally interest in an item will vary around a small area, but occasionally it will jump. Then we run it on the data. This model will find interesting events, like times when there was a service interruption, or when the page got linked from some source, etc. I.e., it can detect discrete events that are important to the history of interest in the item.