| Tags: |
|---|
Support Vector Machine Learning for Interdependent and Structured Output Spaces
Ioannis Tsochantaridis, Thomas Hofmann, Thorsten Joachims, Yasemin Altun. Proceedings of the 21st International Conference on Machine Learning. 2004.
Summary
This article presents a generalization of SVMs that can be used to learn mappings whose outputs are complex structures. The approach they take is to find a function F which maps (input,output) pairs to scores or probabilities; and then to select the output to maximize the score among the pairs with the correct input value. They then use margin constraints to find the 'best' F function within a paramaterized space (linear combinations of feature functions of the input & output).
This approach can then be applied to a variety of output types (although it appears to be fairly slow on parsing, given the size of training & test sets they used).
Algorithm
Descriminant
First, they define a discriminant function F, which maps (input, output) -> real. They assume that this discriminant function can be decomposed into a linear combination of features:
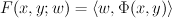
where <,> is the dot product; w is a weight vector; and phi is a 1-dimentional array of feature functions.
In this context, the problem of finding the right discriminant function reduces to finding the right values for the weight vector. To do this, they use a margin maximization technique.
Constraints
They define a set of constraints, which they will use in the margin maximization. For each training sample, they define the constraints:
∀j ∀i, i≠j: <w,phi(xi,yj)> < <w,phi(xi,yi)>
This is a very large set of constraints (the square of the number of training examples), but they will find a smaller set of constraints that approximate this set.
Given these constraints, they basically find the minimum-length weight vector (w) that satisfies them, which gives them the maximum margin.
They also give a modification that allows for soft-margins, by adding slack variables.
Learning
See the paper for details. They use a given loss function to pick which constraints to add.
Applications
They apply their method to multiclass classification, classification w/ taxonomies, label sequence learning, sequence alignment, and parsing.
Comments
This is a very interesting learning algorithm. The question of how to break a problem down into smaller problems basically becomes a question of feature selection, in this vector of features phi. In their examples, they generally assume that these feature functions have fairly simple regular structures, which they use to break them down.
This approach requires that the output features can be divided up in some sort of linear way. I'm not sure yet exactly what the implications of that requirement are. It also means that all output features are basically treated uniformly.